

Biomechanics
Biomechanics is the science concerned with the internal and external forces acting on the human body and the effects produced by these forces.
Kinetics is a study of the cause of motion, namely forces and torques, e.g. forces between the feet and the ground when jumping. Kinematics is the study of movement regarding the time taken to carry out the activity.
Distance and displacement
Distance (length of the path a body follows) and displacement (length of a straight line joining the start and finish points) are quantities used to describe a body's motion. e.g. in a 400m race on a 400m track, the distance is 400 metres, but their displacement will be zero metres (start and finish at the same point).
Speed and velocity
Speed and velocity describe the rate at which a body moves from one location to another. The average speed of a body is obtained by dividing the distance by the time, and average velocity is obtained by dividing the displacement by the time, e.g. a swimmer in a 50m race in a 25m long pool who completes the race in 71 seconds - distance is 50m, and displacement is 0m (swimmer is back where they started), so the speed is 50/71= 0.70m/s and velocity is 0/71=0 m/s
- Speed and Velocity = distance travelled ÷ time taken.
Acceleration
Acceleration is defined as the rate at which velocity changes with respect to time.
- average acceleration = (final velocity - initial velocity) ÷ elapsed time
From Newton's 2nd law:
- Force = Mass x Acceleration
- Acceleration = Force ÷ Mass
If the mass of a sprinter is 60kg and the force exerted on the starting blocks is 600N, then acceleration = 600 ÷ 60 = 10 msec².
Acceleration due to gravity
While a body is in the air, it is subject to a downward acceleration, due to gravity, of approximately 9.81m/s².
Vectors and scalars
Distance and speed can be described in magnitude (amount) and are known as scalars. Displacement, velocity, and acceleration require magnitude and direction, known as vectors.
Components of a vector
 Figure 1 |
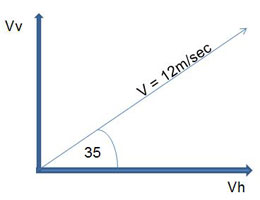 Figure 2 |
Let us consider the horizontal and vertical components of the velocity of the medicine ball in Figure 1.
Figure 2 indicates the angle of release of the medicine ball is 35°, and the velocity at release is 12 metres/second.
- Vertical component Vv = 12 x sin 35° = 6.88 m/sec.
- Horizontal component Vh = 12 x cos 35° = 9.82 m/sec.
Let us now consider the distance the medicine ball will travel horizontally (its displacement).
Distance (D) = ((v² × sinØ × cosØ) + (v × cosØ × sqrt ((v × sinØ)² + 2gh))) ÷ g.
Where v = 12, Ø = 35, h = 2m (height of the shot above the ground at release) and g = 9.81.
- D = ((12² × sin35 × cos35) + (12 × cos35 × sqrt ((12 × sin35)² + 2 x 9.81 x 2))) ÷ 9.81.
- D = 16.22m.
The time of flight of the shot can be determined from the equation:
- Time of flight = Distance (D) ÷ velocity (Vh) .
- Time of flight = 16.22 ÷ 9.82 = 1.65 seconds.
Uniformly accelerated motion
When a body experiences the same acceleration throughout an interval of time, its acceleration is said to be constant or uniform, and the following equations apply:
- Final velocity = initial velocity + (acceleration x time).
- Distance = (initial velocity x time) + (½ x acceleration x time²).
Moment of force (torque)
The moment of force or torque (τ) is the application of a force at a perpendicular distance to a joint or point of rotation.
Torque (τ = rFsin θ) depends on three quantities:
- The length of the lever arm connecting the axis to the point of force application (r).
- The force applied (F).
- the angle between the force vector and the lever arm (sin θ).
Angular Kinematics
Angular distance and displacement
When a rotating body moves from one position to another, the angular distance through which it moves is equal to the angular path's length. The angular displacement that a rotating body experiences is similar to the angle between the body's initial and final position.
Angular movement is usually expressed in radians where 1 radian = 57.3°
Angular speed, velocity and acceleration
- Angular speed = angular displacement ÷ time.
- Angular velocity = angular displacement ÷ time.
- Angular acceleration = (final angular velocity - initial angular velocity) ÷ time.
Angular Momentum
Angular momentum is defined as angular velocity x moment of inertia.
The angular momentum remains constant throughout a movement, provided nothing outside the system acts with a turning moment. This is known as the Law Conservation of Angular Momentum. (e.g. if a skater, when already spinning, moves their arms out to the side, then the rate of spin will change, but the angular momentum will stay the same).
Linear Kinetics
Kinetics is concerned with what causes a body to move.
Momentum, inertia, mass, weight and force
- Momentum: mass x velocity.
- Inertia: the reluctance of a body to change whatever it is doing.
- Mass: The quantity of matter of which a body is composed - not affected by gravity - measured in kilograms (kg).
- Weight: force due to gravity -9.81m/s².
- Force: a pushing or pulling action that causes a change of state (rest/motion) of a body is proportional to mass x acceleration. It is measured in Newtons (N), where 1N is the force that will produce an acceleration of 1 m/s² in a body of 1kg mass.
The classification of external or internal forces depends on the definition of the 'system'. In biomechanics, the body is seen as the 'system', so any force exerted by one part of the system on another part of the 'system' is known as an internal force. All other forces are external.
Newton's Laws of Motion[1]
- First Law: Every body continues in its state of rest or motion in a straight line unless compelled to change that state by external forces exerted upon it.
- Second Law: The rate of change of momentum of a body is proportional to the force causing it, and the change takes place in the direction in which the force acts.
- Third Law: For every action, there is an equal and opposite reaction OR for every force that is exerted by one body on another, there is an equal and opposite force exerted by the second body on the first.
Newton's law of gravitation[1]
- Any two particles of matter attract one another with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Kinetic Energy and Power
Kinetic energy is the mechanical energy possessed by a moving object.
Kinetic Energy = ½ x mass x velocity² (joules).
Power is defined as the rate at which energy is used or created from other forms.
- Power = energy used ÷ time taken.
- Power = (force x distance) ÷ time taken.
- Power = force x velocity.
Angular Kinetics
Translation and couple
A force that acts through the centre of a body results in movement (translation). A force whose line of action does not pass through the body's centre of gravity is called an eccentric force and results in movement and rotation.
For example, if you push through the centre of an object, it will move forward in the force's direction. If you push to one side of the object (eccentric force), it will move forward and rotate.
A couple is an arrangement of two equal and opposite forces that cause a body to rotate.
Levers
A lever is a rigid structure hinged at one point and to which forces are applied at two other locations. The two forces that act on the lever are the weight that opposes movement and the force that causes movement. The hinge is known as the fulcrum. For more details, see the page on Levers.
Bernoulli Effect
If an object has a curved top and flat bottom (e.g. the wing of an aircraft), the air will have to travel over the top of the wing more than the bottom. For the two airflows to reach the rear of the wing simultaneously, the air flowing over the top of the wing will have to flow faster, resulting in less pressure above the wing (air is thinner) than below it, and the aircraft will lift. This is known as the Bernoulli effect.
References
- HAY, J. G. (1993) The Biomechanics of Sports Technique. 4th Ed. London, Prentice-Hall International (UK) Ltd. p. 64-68
Page Reference
If you quote information from this page in your work, then the reference for this page is:
- MACKENZIE, B. (2004) Biomechanics [WWW] Available from: https://www.brianmac.co.uk/biomechanics.htm [Accessed